The Gyrojet was a cool line of firearms that used tiny rockets as bullets. The projectile would be fired from a lightweight gun with ports along its barrel, and accelerate over the course of its flight. Very cool! I want one but it's about impossible to find ammo anymore, and when you do, it costs about $100 per round!
I encountered this article (reprinted from Small Arms Review, captured at archive.org because the site is gone now) which discussed velocity measurement of Gyrojet projectiles. A large part of the article claims that their measurements showed that the Gyrojet bullets had a strong initial acceleration "which were much higher than expected. Instead of linear acceleration, the rocket’s acceleration rate was fastest at the muzzle and then declined rapidly."
However, a closer look at the authors' own raw data show that their mathematical analysis of the acceleration was wrong, and that their measurements, when analyzed correctly, clearly demonstrate that the acceleration starts out low and increases continuously. Their miscalculations caused them to claim an initial "acceleration anomaly" which simply isn't there. This article adds to the many myths about Gyrojet performance that are not borne out by the researchers' own data.
Let's see how they calculated deceptive, incorrect figures, and calculate the true accelerations over the projectile's flight.
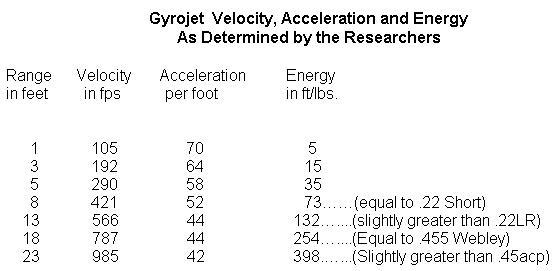
Here's their raw data:

We will assume that the "range in feet" column and "velocity in fps" are correctly-measured quantities. However, they use these to calculate an "acceleration per foot" value whose units of measure are unexplained, and which lead to false interpretations. Also note that the proper units for kinetic energy should be ft·lbf. I'm not sure how accurate their estimates are for kinetic energy; the mass of the bullet would continually change as propellant was burned.
Acceleration per distance, (however it was calculated) is a deceptive measure as it doesn't take into account effects of velocity and is physically unjustified as a metric. In the later parts of its flight, the rocket is moving much faster and spends much less time crossing any given distance, so its velocity will change less in that distance. Acceleration is the change in velocity with respect to time, not distance. Its true acceleration is what we should be calculating, and we will rapidly see how acceleration actually increases over the course of the flight using their same data!
(By the way, I have no idea how they calculated their "acceleration per foot" values. Nothing I can do to torture the numbers with any sensible interpretation gives anything even resembling the trend they calculate.)
The original article also says:
"Based on MBA’s supplied data regarding the maximum Gyrojet velocity and the propellant’s stated burn-time, the researchers expected a Gyrojet rocket to accelerate linearly at the rate of approximately 21 feet per second, per foot of forward rocket travel."
I have no idea what they mean by "accelerate linearly" in this context. If you mean constant acceleration, then you would in no way expect the same change in velocity over a unit distance. I can't invent any reasonable model that would give these results. Since the authors did not post any equations backing this expectation, we may never know why they expected this. No model of constant acceleration would produce such results.
Acceleration is calculated as a=Δv/Δt, that is the change in velocity per change in time. We can calculate the difference in velocity, Δv, directly by subtracting the readings between successive chronographs: Δv=v2 - v1.
We then need to calculate the estimated time to travel between successive chronographs, as this was not timed directly. The time is calculated by first calculating an average velocity between successive chronographs: vavg = (v1 + v2)/2. For a constant acceleration, this will give exactly correct results.
The time spent traveling between chronographs is thus Δt = (d2-d1)/vavg.
From this, we can calculate the average acceleration between each pair of chronographs. The final equation is a=(v2-v1)/((d2-d1)/ ((v1+v2)/2)), which can be simplified to (v12 - v22)/(2 (d1-d2))
| Range (feet) | Velocity (ft/s) | Δt (ms) | Total time (ms) | Acceleration (gee) |
|---|---|---|---|---|
| 0 | 0 | |||
| 19.0 | 19.0 | 171 | ||
| 1 | 105 | |||
| 13.5 | 32.5 | 201 | ||
| 3 | 192 | |||
| 8.3 | 40.8 | 367 | ||
| 5 | 290 | |||
| 8.4 | 49.3 | 482 | ||
| 8 | 421 | |||
| 10.1 | 59.4 | 445 | ||
| 13 | 566 | |||
| 7.4 | 66.8 | 929 | ||
| 18 | 787 | |||
| 5.6 | 72.4 | 1090 | ||
| 23 | 985 | |||
When acceleration is calculated properly, we can see clearly that the data shows that acceleration increases continuously and significantly over the bullet's flight! There is no evidence of a higher initial acceleration "anomaly" -- quite the reverse! The acceleration starts at 171 gees at the beginning of flight, and increases up to 1090 gees through the last chronograph.
There are reasons to expect that acceleration would increase as the bullet lost fuel mass, as combustion temperature increased, and as the nozzle openings eroded, allowing faster release of gas. It's surprising how much the accleration increases over the projectile's flight, even with increasing drag as the speed increases (drag is approximately proportional to the square of the velocity, then there's "wave drag" which may increase drag by a factor of 4 around supersonic speeds. Note that the final speed measured is 90% the speed of sound, into the regime where wave drag becomes significant, yet the acceleration was still increasing.)
Chronograph readings may become rather unreliable with Gyrojet rockets; chronometers assume that the bullet is at approximately constant velocity, while a Gyrojet projectile may be accelerating at over 1000 gees! Other researchers have hinted to me in private communications that some chronographs may have trouble measuring gyrojet projectile velocities accurately, perhaps due to what they characterized as "muzzle flash" or hot gases and metal particles being ejected backwards from the accelerating projectile. Perhaps high-speed photographic analysis of the bullets' flight would be the only way to easily measure, and that's getting hard as bullets become scarce.
Note: In Frink notation, the accelerations can be calculated as:
a[d1, v1, d2, v2] := (v2-v1)/((d2-d1)/ ((v1+v2)/2))
a[1 ft, 105 ft/s, 3 ft, 105 ft/s] -> gee
You can also see the full Frink program used to generate the table above at gyrojet.frink.
There is now some 4K video showing Gyrojets being shot in super-slow-motion!
I Accidentally Blew Up My Gyrojet (YouTube)